KINEMATIC CHAIN
a) Kinematic chain: A kinematic chain is an assembly of links which are interconnected through joints or pairs, in which the relative motions between the links is possible and the motion of each link relative to the other is definite.
b) Non-kinematic chain: In case the motion of a link results in indefinite motions of others links, it is a non-kinematic chain. The reason for this indefinite motion lies in the fact that if we give motion to any of the link in the chain then the other links can take indefinite position.
c) Redundant chain: There is no motion possible in the redundant chain. It can be observed from the figure c that this chain is locked due to its geometry.
DEGREE OF FREEDOM IN A MECHANISM
Degrees of freedom of a mechanism in space can be explained as follows:
Let
N = total number of links in a mechanism
F = degrees of freedom
J1 = number of pairs having one degree of freedom
J2 = number of pairs having two degree of freedom and so on.
When one of the links is fixed in a mechanism
Then, the number of the movable links are = N – 1
Degrees of freedom of (N- 1) movable links = 6(N-1)
(Because each movable link has six degree of freedom) Each pair having one degree of freedom imposes 5 restraints on the mechanism reducing its degrees of freedom by 5J1 this is because of the fact that the restraint on any of the link is common to the mechanism as well. Other pairs having 2, 3, 4 and 5 degrees of freedom reduce the degree of freedom of the mechanism by putting constraints on the mechanism as well.
Then, the DOF can be given by
F = 6(N-1) – 5J1 – 4J2 – 3J3 – 2J4 – 1J5
Most of the mechanism we generally study are two dimensional in nature, such as slider-crank mechanism in which translatory motion is possible along two axes(one restraint) and rotary motion about only one axis(two restraints).Thus there are three general restraints in a two dimensional mechanism. This can be shown with the help of figure that a link has three degree of freedom in two dimensions.
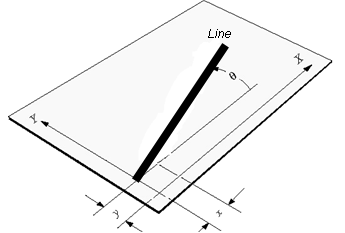 |
| a line in a plane has three DOF: x, y, θ |
Therefore, for plane mechanism, the following relation can be used for degrees of freedom,
F = 3 (N-1) – 2J1 – 1J2
This equation is known as Gruebler’s criterion for degrees of freedom of plane mechanism. It should be noted here that gruebler’s criterion does not take care of geometry of the mechanism so it can give wrong prediction. So, inspection should be done in certain cases to find the degrees of freedom.

